Octopus
February 10, 2021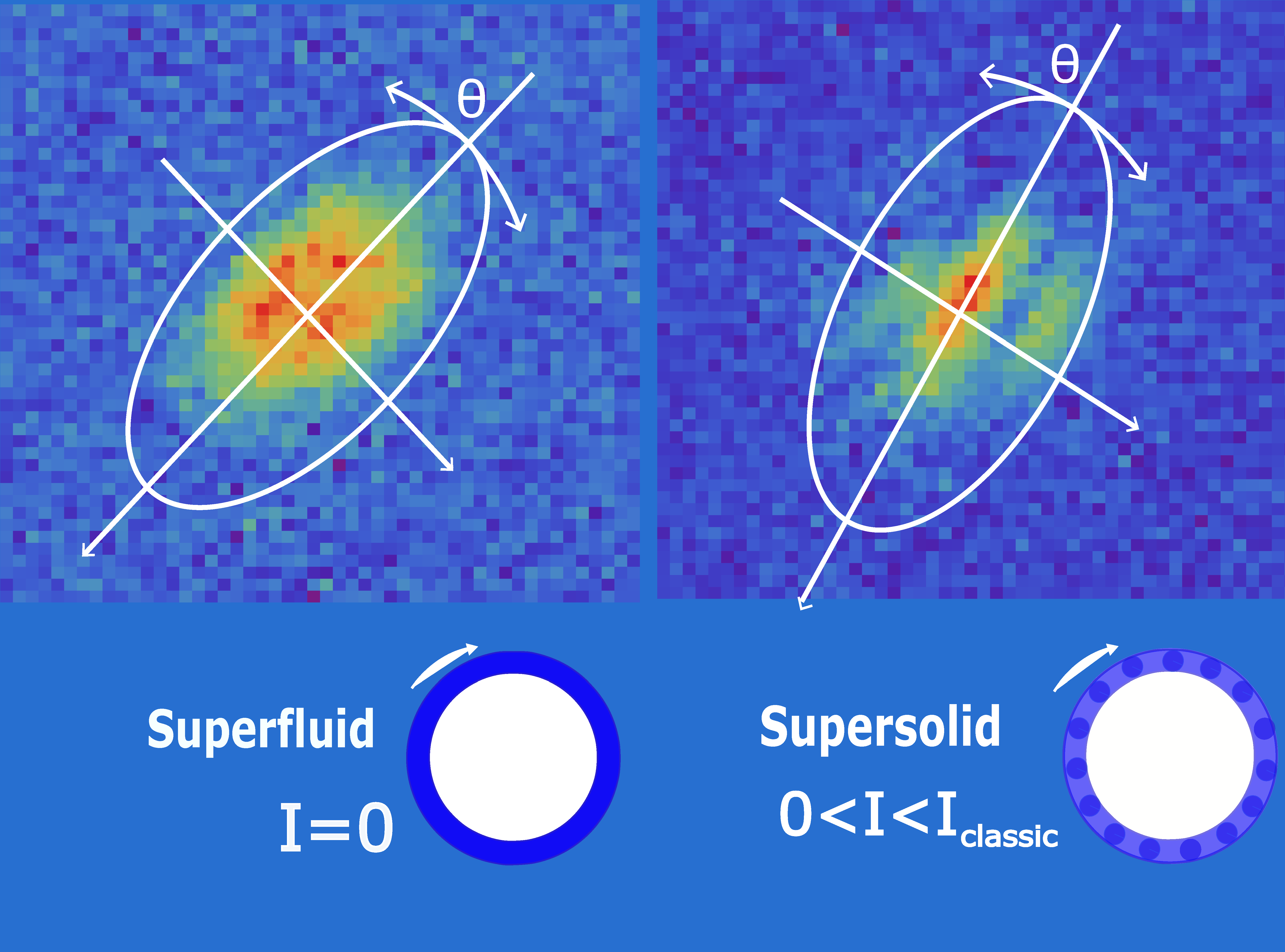
Il supersolido ruota senza inerzia
March 25, 2021L’articolo “On the destabilization of a periodically driven three-dimensional torus” di Euzzor, A. Di Garbo, J.-M. Ginoux, S. Zambrano, F. T. Arecchi, R. Meucci è stato appena pubblicato sulla rivista International Journal Nonlinear Dynamics, DOI 10.1007/s11071-020-06174-5. Gli autori hanno sperimentalmente dimostrato la transizione al caos in un toro tridimensionale usando una piccola perturbazione sinusoidale con controllo della fase relativa. Questo risultato è di fondamentale importanza perché può essere ricondotto direttamente allo scenario di Ruellle e Takens per la transizione al caos nei sistemi dissipativi ma anche al Teorema KAM (acronimo per Kolmogorov, Arnol’d e Moser). Quest’ultimo teorema è di fondamentale importanza nella teoria dei sistemi dinamici perché garantisce la stabilità di soluzioni quasi-periodiche (ossia di tori invarianti, detti anche tori KAM) anche in presenza di piccole perturbazioni che rendono il sistema non integrabile. In altri termini, le soluzioni del sistema imperturbato continuano ad esistere, sebbene deformate, anche nel sistema perturbato. Questo implica, nel caso considerato, che la transizione al caos non avvenga in modo immediato e completo ma in maniera “smooth”. Notevoli sono le applicazioni del Teorema KAM a partire dalla stabilità del moto dei corpi celesti (problema dei tre corpi) e a quella degli acceleratori tokamak. Passando alle applicazioni quantistiche, il corrispondente quantistico del Teorema KAM è stato dimostrato nella dinamica a molti corpi in un gas di Bose unidimensionale.